Fairness is a highly subjective concept and is not different when comes to machine learning. We typically feels that the referees are “unfair” to our favorite team when they lose a close match or that any outcome is extremely “fair” when it goes our way. Given that machine learning models cannot rely on subjectivity, we need an efficient way to quantify fairness. A lot of research has been done in this area mostly framing fairness as an outcome optimization problem. Recently, Google AI research open sourced the Tensor Flow Constrained Optimization Library(TFCO), an optimization framework that can be used for optimizing different objectives of a machine learning model including fairness.

The problem of introducing fairness is machine learning models is far from being an easy one. A very public example of this was seen in the recent case of the Apple Card in which the algorithms showed a strong gender-bias. Consider a similar model that process loan applications for a bank. Should the model optimize to grant loans to customers that are likely to pay or minimize denying loans to customers based on the wrong criteria. Which criteria is more costly? Could a model possibly optimize for both outcomes? These questions are at the heart of the TFCO design.

The TFCO Theory

TFCO works by imposing “fairness constraints” around the objectives of a given model. In our bank loan example, TFCO, we would choose an objective function that rewards the model for granting loans to those people who will pay them back, and would also impose fairness constraints that prevent it from unfairly denying loans to certain protected groups of people. TFCO achieves that by leveraging an highly sophisticated game theory known as “Proxy Lagrangian Optimization”.

The ideas behind the proxy Lagrangian optimization technique were outlined in a recent collaboration between Google Research and Cornell University. The core principle focuses on optimizing the Lagrange multipliers in a model. These multipliers are the basics of a strategy for finding the local maxima and minima of a function subject to equality constraints (i.e., subject to the condition that one or more equations have to be satisfied exactly by the chosen values of the variables). The basic idea is to convert a constrained problem into a form such that the derivative test of an unconstrained problem can still be applied.

The Lagrange multiplier theorem roughly states that at any stationary point of the function that also satisfies the equality constraints, the gradient of the function at that point can be expressed as a linear combination of the gradients of the constraints at that point, with the Lagrange multipliers acting as coefficients.

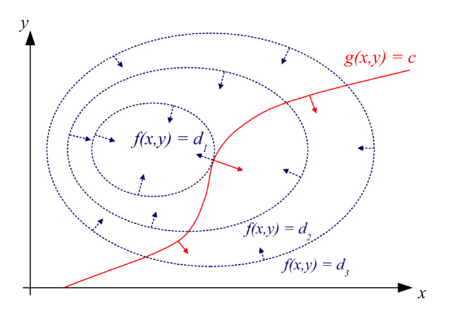
TFCO expands on the idea of Lagrange multipliers by modeling out an optimization problem as a two-player game played between a player who seeks to optimize over the model parameters, and a player who wishes to maximize over the Lagrange multipliers. me. The first player minimizes external regret in terms of easy-to-optimize “proxy constraints”, while the second player enforces the original constraints by minimizing swap regret. In other words, The first player chooses how much the second player should penalize the (differentiable) proxy constraints, but does so in such a way as to satisfy the original constraints.

To illustrate the principles of TFCO, let’s use a couple of visualizations based on a traditional classifier with two protected groups: blue and orange. Instructing TFCO to minimize the overall error rate of the learned classifier for a linear model (with no fairness constraints), might yield a decision boundary that looks like this:

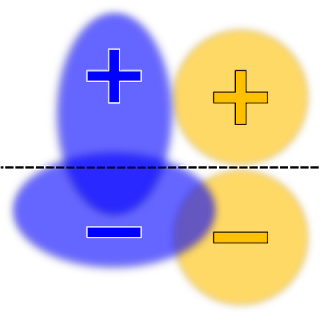
Under different circumstances, that model can be considered to be unfair. For example, positively-labeled blue examples are much more likely to receive negative predictions than positively-labeled orange examples. A constraints that maximizes the equality of opportunity, or the true positive rate, could be added changing the model to the following distribution:

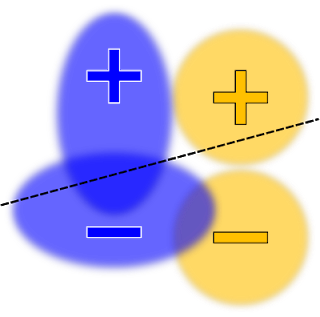
A similar optimization that optimizes both the true positive rate and false positive rate constraints will look like the following:

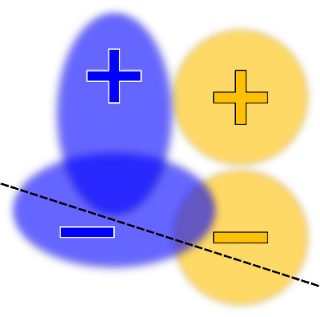
Ultimately, choosing the right constraints is a complex exercise that highly depends on the policy goals and the specific nature of the machine learning problem. For example, suppose one constrains the training to give equal accuracy for four groups, but that one of those groups is much harder to classify. In this case, it could be that the only way to satisfy the constraints is by decreasing the accuracy of the three easier groups, so that they match the low accuracy of the fourth group. This probably isn’t the desired outcome. To address this challenge, TFCO includes a series of curated optimization problems.

From the developer experience perspective, using TFCO is a relatively simple experience. The first step is to import the TFCO library:

import tensorflow as tf
import tensorflow_constrained_optimization as tfco

After that, we need to express a model as an optimization problem as shown in the following code.

# Create variables containing the model parameters.
weights = tf.Variable(tf.zeros(dimension), dtype=tf.float32, name="weights")
threshold = tf.Variable(0.0, dtype=tf.float32, name="threshold")

# Create the optimization problem.
constant_labels = tf.constant(labels, dtype=tf.float32)
constant_features = tf.constant(features, dtype=tf.float32)
def predictions():
  return tf.tensordot(constant_features, weights, axes=(1, 0)) - threshold

Ultimately, TFCO focuses on optimizing constrained problems written in terms of linear combinations of rates, where a “rate” is the proportion of training examples on which an event occurs (e.g. the false positive rate, which is the number of negatively-labeled examples on which the model makes a positive prediction, divided by the number of negatively-labeled examples). Once we have a model represented as an optimization problem, we can use TFCO to create different optimizations such as the following:

# Like the predictions, in eager mode, the labels should be a nullary function
# returning a Tensor. In graph mode, you can drop the lambda.
context = tfco.rate_context(predictions, labels=lambda: constant_labels)
problem = tfco.RateMinimizationProblem(
    tfco.error_rate(context), [tfco.recall(context) >= recall_lower_bound])

TFCO is an initial release and still requires quite a bit of optimization knowledge. However, it provides a very flexible foundation to incorporate fairness constraints in machine learning models. Its going to be interesting to see what the TensorFlow community builds on top of it.

Post source: https://towardsdatascience.com/google-open-sources-tfco-to-help-build-fair-machine-learning-models-f6d002557796